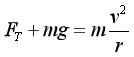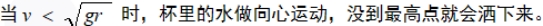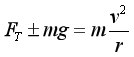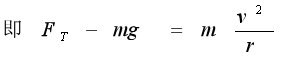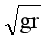ShaYun - 沙云

主备课人

授课人

课  题

专题1 竖直面内的圆周运动

课时

1课时

课型

新授

教学目标

（学科核心素养）

1、理解竖直面内的圆周运动问题的模型特点、特殊点的受力分析。

2、能够根据实际情景分析向心力的来源，以及临界状态，计算出临界值。

教学重点

理解竖直面内的圆周运动问题的模型特点、特殊点的受力分析。

教学难点

能够根据实际情景分析向心力的来源，以及临界状态，计算出临界值。

易错点

教学方法

讲授法，逻辑分析法，情境导入法，

教    学    设    计

一  次  备  课

二次备课

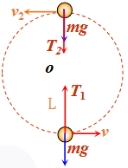
【情境导入】

思考：为什么在最高点时过山车没有掉下来？

      为什么杯子倒过来的时候水没有流出来？

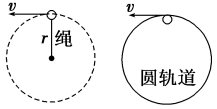
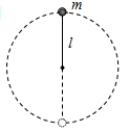
物体在竖直面内做的圆周运动是一种典型的变速曲线运动，该类运动常常会涉及临界问题，并伴有“最大”“最小”“刚好”等词语，常见模型有两种：轻绳小球模型和轻杆小球模型。

一、绳(轨)球模型

由轻绳（或内轨道）与小球组成无支撑的物理模型。

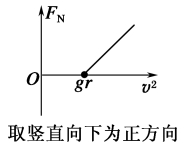
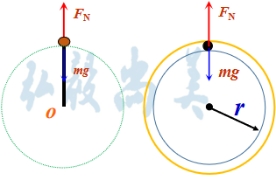
绳约束   光滑内轨道约束

1、绳(内轨道)施力特点：(1).只能施加指向圆心的拉力(或压力)；

(2).最高点的动力学方程：。

2、最高点的分析：

在最高点的F_N－v²图线：

3、最低点的分析：(超重)

，

可见，此时绳的拉力最大，若小球通过最低点的速度过大细线可能被拉断。

【实例分析】——水流星表演

【实例分析】——过山车

思考：过山车为什么过最高点时不会掉下来？

播放游乐场里的过山车、实验室的过山车的视频。

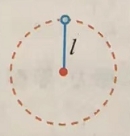
【例题讲解】

如图所示，一质量为m=0.5kg的小球，用长为l=0.4m的细线拴住在竖直面内作圆周运动．取g=10m/s2．试求：

（1）当小球在圆上最高点速度v1=4m/s时，细线的拉力．

（2）若轻绳能承受的最大张力为45N，求小球的速度不能超过多大值？

二、杆(管)球模型

由轻杆（或管道）——小球组成有支撑的物理模型。

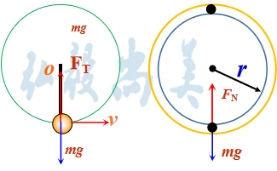
杆约束   光滑管道约束

1、杆(管)施力特点：(1)可拉、可压，可向上、可向下；

(2)最高点的动力学方程：

2、最高点的分析：

由于杆和管在最高处能对小球产生向上的支持力，故小球恰能到达最高点的最小速度v＝0，此时小球受到的支持力F_N＝mg.

3、最低点的分析：(超重)

可见，此时杆的拉力(或环的支持力）最大。

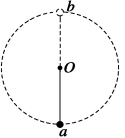
【例题讲解】

如图所示，细杆的一端与小球相连，可绕过O点的水平轴自由转动，细杆长0.5m，小球质量为3kg，现给小球一初速度使它做圆周运动，若小球通过轨道最低点a的速度为va＝4m/s，通过轨道最高点b的速度为vb＝2m/s，取g＝10m/s2，则小球通过最低点和最高点时对细杆作用力的情况是（　　）

A．在a处为拉力，方向竖直向下，大小为120N

B．在a处为压力，方向竖直向上，大小为120N

C．在b处为拉力，方向竖直向上，大小为6N

D．在b处为压力，方向竖直向下，大小为6N

【本节小结】

【布置作业】

学案的三个题。

板书设计

专题1 竖直面内的圆周运动

一、绳模型

在最高点，线速度 V≥

二、杆模型

在最高点，线速度 V≥0

教学反思